Answer: The 100th even natural number is 200.
Step-by-step explanation: Given that the following arithmetic sequence represents the set of natural numbers :
2, 4, 6, 8, 10, . . ..
We are given to find the 100th even natural number, i.e., the 100-th term of the sequence.
We know that
the n-th term of an arithmetic sequence with first term a and common difference d is given by
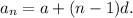
For the given sequence, we have
a = 2 and d = 4 - 2 = 6 - 4 = . . . =2.
Therefore, the 100-th term of the sequence will be
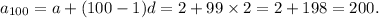
Thus, the 100th even natural number is 200.