Question

The midpoint of a segment is (6,−6) and one endpoint is (13,−1). Find the coordinates of the other endpoint.

Answer 1

(-1, -11)
13 is 7 away from 6, and -1 is 5 away from 6. Subtract 7 away from 6, and 5 away from -6.

Answer 2

Answer: The other endpoint of the segment is (-1, -11).

Step-by-step explanation: Given that the midpoint of a line segment is (6, -6) and one endpoint is (13, -1).

We are to find the co-ordinates of the other endpoint.

Let (a, b) be the co-ordinates of the other end-point.

Then, according to the given information, we have

`\left((a+13)/(2),(b+(-1))/(2)\right)=(6,-6)\\\\\\\Rightarrow \left((a+13)/(2),(b-1)/(2)\right)=(6,-6).`

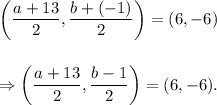
Equating the x and y co-ordinates on both sides of the above, we get

`(a+13)/(2)=6\\\\\\\Rightarrow a+13=12\\\\\Rightarrow a=12-13\\\\\Rightarrow a=-1`

and

`(b-1)/(2)=-6\\\\\\\Rightarrow b-1=-12\\\\\Rightarrow b=-12+1\\\\\Righatrrow b=-11.`

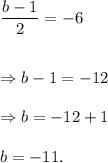
Thus, the other endpoint of the segment is (-1, -11).