Answer:
Number of luxury gift tins of biscuits L sold is 18.
Number of mini- packs of 2 biscuits M sold is 80.
Number of normal packets N sold is 2.
Explanation:
Let L, M, N represent the number of Luxury, Mini, and Normal packets sold.
Total earned by selling luxury gift tins of biscuits = 5L
Total earned by selling normal packets = £1N
Total earned by selling 2 biscuits at 10p = 0.1M
Marianne tells Amy that she has received exactly 100 donations in total:
Equation becomes:
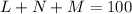 .... (1)
.... (1)
total earning is £100, so another equation becomes:
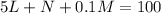 .......(2)
.......(2)
Given is that stock of £1 packets is very low compared with the other items:
so, N<L and N<M
Putting y = 0 in equation 1 and 2
 or
or
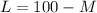 .....(3)
.....(3)
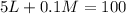 ......(4)
......(4)
Replacing L by 100-M in the equation 4

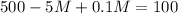
4.9M=400
M=81.63
As, L=100-M
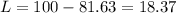
L=18.37
We can round L and M to 18 and 81 respectively and solve for N from 1 and 2 equations.

=>

=>
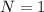
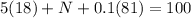
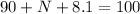
=> N=1.9
We will repeat the same process with N = 2 and get the following result.
Number of luxury gift tins of biscuits L sold is 18
Number of mini- packs of 2 biscuits M sold is 80
Number of normal packets N sold is 2