Question

Can you please explain the correct answer

Answer 1

(A)
`AC=10sin40^(\circ)`

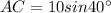
Explanation:

From the given figure, it is given that ABC is a right angled triangle which is right angled at C and AC=b, CB=a and AB=10in.

Now, using the trigonometry, we have

`(AC)/(AB)=sinB`

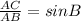
Substituting the given values, we have

`(AC)/(10)=sin40^(\circ)`

`AC=10sin40^(\circ)`

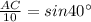
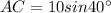
Thus, the above equation can be used to find the value of AC, therefore

⇒
`b=10sin40^(\circ)`

⇒
`b=10(0.642)`

⇒
`b=6.42 in`

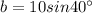
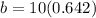
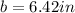
Thus, the value of AC is 6.42 inches.

Answer 2

For this case we have as data:
1) hypotenuse of the triangle
2) Angle between the base of the triangle and the hypotenuse.
Therefore, we can use the following trigonometric relationship:

`sine (40) = AC / 10`
From here, we clear the value of AC.
We have then:

`AC = 10 * sine (40)`
Answer:
The encuacion that can be used to find the length of AC is given by:

`AC = 10 * sine (40)`
option 1