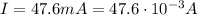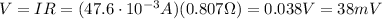Question

Find the Voltage drop (in mV) across an 46.6 m long copper wire with diameter of 1.11 mm and with 47.6 miliAmps of current running through it. (The resistivity of copper at room temperature is 1.68×10-8 Ohm×meter). Express the answer (only numerical value) to the nearest whole number.

Answer 1

First we need to calculate the resistance of this piece of wire. For a wire with resistivity
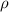
`\rho`, length L and cross section A, the resistance is

`R= (\rho L)/(A)`
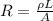
The diameter d of the wire is
`d=1.11 mm=1.11 \cdot 10^(-3) m`, so the cross sectional area is

`A=\pi ( (d)/(2) )^2=9.7 \cdot 10^(-7) m^2`
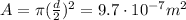
Now, using
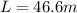
`L=46.6 m` and
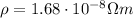
`\rho=1.68 \cdot 10^(-8) \Omega m`, we can calculate the resistance:

`R= (\rho L)/(A)= ((1.68 \cdot 10^(-8) \Omega m)(46.6 m))/(9.7 \cdot 10^(-7)m^2) =0.807 \Omega`

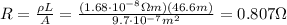
And now we can calculate the voltage drop across the resistor, by using Ohm's law, since we know the current flowing through it:
`I=47.6 mA=47.6 \cdot 10^(-3) A`

`V=IR=(47.6 \cdot 10^(-3) A)(0.807 \Omega)=0.038 V=38 mV`