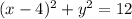Answer:
Equation of the circle is
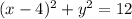
Explanation:
We have been given that
center of the circle = (4,0)
Radius of the circle =
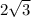
The standard form of a circle is given by
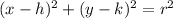
Here, (h,k) is the center and r is the radius. Thus, we have
h = 4, k = 0, r = 2√(3)
Substituting these values in the above equation, we get
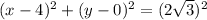
Simplifying, we get
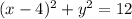
Therefore, equation of the circle is