Question

A $6,000.00 principal earns 8% annual interest, compounded semiannually (twice per year). After 35 years, what is the balance in the account?

A. $22,800.00
B. $39,600.00
C. $88,712.07
D. $93,429.71

Answer 1

if im not wrong then i sure its C

Answer 2

After 35 years balance in the account = $93429.71

Step-by-step explanation:

We will applying the compound interest formula.

A =
`P(1 +(r)/(n))^(nt)`

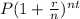
Where,

A = the future value of the investment/loan, including interest

P = the principal investment amount (the initial deposit or loan amount)

r = the annual interest rate (decimal)

n = the number of times that interest is compounded per year

t = the number of years

Given that,

P = $6000

r = 8% =
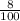`(8)/(100)` = 0.08

n = 2 (because of twice in a year)

t = 35 years

`A= 6000(1 + (0.08)/(2)) ^(2*35)`

A = 6000
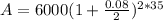
`(1.04)^(70)`

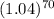
A= $93429.71 (Option D)