Question

Help me pls asap!! it’s pass due!
Simplify the expression and rationalize the denominator.

Answer 1

Answer: C

Explanation:

First, take the square root of both the numerator and denominator. The numerator would then be equal to 6 a^4 b^2 and the bottom would just be sqrt7c. Since you still have a sqrt in the denominator, rationalize the fraction by multiplying sqrt7c to both the numerator and denominator to get rid of the sqrt. This would leave you with answer choice C.

Answer 2

`(6a^4b^2√(7c))/(7c)`

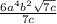
Explanation:

You can distribute radicals across division such that:
`\sqrt[n]{(a)/(b)}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}`

So you get the expression:
`(√(36a^8b^4))/(√(7c))`

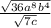
Similarly with division, you can distribute radicals across multiplication such that:
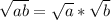`√(ab)=√(a)*√(b)`, and you can do this multiple times

So our expression on top becomes:
`(√(36)*√(a^8)*√(b^4))/(√(7c))`

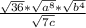
Whenever we take the square root of a base to an exponent, we simply divide the exponent by two. In general if you take the "nth" root of any base to an exponent, you divide the exponent by n, since:
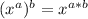`(x^a)^b=x^(a*b)` and radicals such as:
`\sqrt[n]{x}=x^{(1)/(n)}`, so you're just multiplying the two, which results in a division of "n" which in this case is 2.

So the square root of a^8 simplifies to a^4 after dividing the exponent by 2, which makes since:
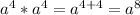`a^4*a^4=a^(4+4)=a^8` which exemplifies the very definition of a square root.

Applying this same logic to b^4 and just simplifying sqrt(36) regularly we get the following expression:

`(6a^4b^2)/(√(7c))`

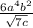
We generally don't want square roots in the denominator, so we rationalize it by multiplying by the sqrt(7c)/sqrt(7c) which just simplifies to one, so we're not actually changing the value but it removes the sqrt(7c) from the denominator

`(6a^4b^2)/(√(7c)) *(√(7c))/(√(7c))\\\\(6a^4b^2√(7c))/(7c)`

and this turns out to be our solution!