Question

How many ways can you pick 4 students from 10 students (6 men, 4 women)?

Answer 1

Consider this option:
for 4 person from 10: C⁴₁₀.
It means C₁₀⁴ =
`(10!)/(4!6!)= (7*8*9)/(4!)= (7*8*9)/(24)=21.`

Answer: 21 ways.

Answer 2

There are 210 ways in which you can pick 4 students from 10 students (6 men, 4 women).

Explanation:

We use the combination formula because the order does not matter.

For example, John, Laura,... is the same way as Laura, then John, then ...

Combinations formula

`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

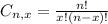
In this problem, we have that:

Combinations of 4 students from a set of 10. So

`C_(10,4) = (10!)/(4!(10-4)!) = 210`

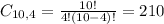
There are 210 ways in which you can pick 4 students from 10 students (6 men, 4 women).