Question

Find the angle formed by two forces of 7N and 15N respectively if its result is worth 20N

Answer 1

First, you need to make certain assumptions before solving this question. Why? Because there are no information given about the direction of these forces. In such questions as above, ALWAYS make the following assumptions:

1) Take first force, say
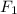
`F_(1)`, and assume that it is pointing towards the x-direction.

Let us take the 7N force! By keeping the above assumption in our minds, the force vector would be like:

`F_(1)` =
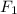
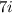
`7i`, where
`i` = Unit vector in the x-direction.

2) Take the second force, say
`F_(2)`, and assume that it is making an angle
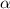
`\alpha` with the first force
`F_(1)`.

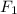
Let us take the 15N force! By keeping the above assumption in our minds, the forces vector would be like:


`F_(2) = (15*cos \alpha)i + (15*sin \alpha )j`

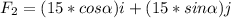
Now from simple vector addition, we know that,

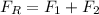
`F_(R) = F_(1) + F_(2)` --- (A)

Where
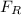
`F_(R)` = Resultant vector.
NOTE: In equation (A), all forces are in vector notation. Assume that there is an arrow head on top of them.

Let us find
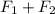
`F_(1)+F_(2)` first!

`F_(1)+F_(2)` =
`7i+(15*cos \alpha)i + (15*sin \alpha )j`

=>
`F_(1)+F_(2)` =
`(7+15*cos \alpha)i + (15*sin \alpha )j`

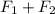
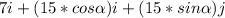
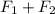
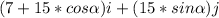
Now the magnitude of
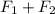
`F_(1)+F_(2)` is,
|
`F_(1)+F_(2)`| =
`\sqrt{ (7+ 15*cos \alpha)^(2) + (15*sin \alpha )^(2)}`

=> |
`F_(1)+F_(2)`| =
`\sqrt{ 49 + 225*(cos \alpha)^(2) + 210*(cos \alpha)+ 255*(sin \alpha )^(2)}`

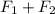
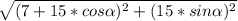
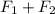
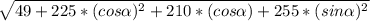
Since
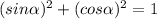
`(sin \alpha)^(2) + (cos \alpha)^(2) = 1`, therefore,

=> |
`F_(1)+F_(2)`| =
`√( 49 + 225 + 210*(cos \alpha))`

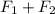
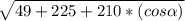
Since |
`F_(1)+F_(2)`| = |
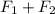
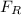
`F_(R)`|, and the magnitude of the resultant force is 20N, therefore,

|
`F_(R)`| = |
`F_(1)+F_(2)`|
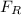
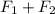
20 =
`√( 49 + 225 + 210*(cos \alpha))`

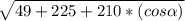
Take square on both sides,
400 =
`49 + 225 + 210*(cos \alpha)`

`(cos \alpha) = (3)/(5)`


`\alpha = 53.13^(o)`

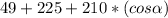
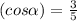
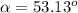Ans: Angle formed by the two forces, 7N and 15N, is: 53.13°

-israr