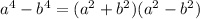Answer:
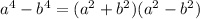
Explanation:
The given expression is
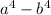
This expression is the difference of two perfect squares, and their square roots are

Now, the difference of two perfect squares can be factored as
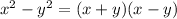
So, if we apply this rule, the result would be
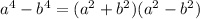
Therefore, the simplest form of the binomial expression is