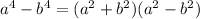Question

What is the simplest form of this binomial expression?

a4 − b4

Answer 1

Answer and work in images

Answer 2

`a^(4)-b^(4)=(a^(2)+b^(2))(a^(2)-b^(2))`

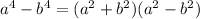
Explanation:

The given expression is

`a^(4)-b^(4)`

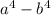
This expression is the difference of two perfect squares, and their square roots are

`\sqrt{a^(4)} =a^(2)\\ \sqrt{b^(4)} =b^(2)`

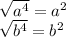
Now, the difference of two perfect squares can be factored as

`x^(2) -y^(2)=(x+y)(x-y)`

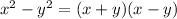
So, if we apply this rule, the result would be

`a^(4)-b^(4)=(a^(2)+b^(2))(a^(2)-b^(2))`

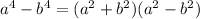
Therefore, the simplest form of the binomial expression is

`a^(4)-b^(4)=(a^(2)+b^(2))(a^(2)-b^(2))`