Answer:
Jillian is not correct
Jillian has summed up the possible number of codes for each digit instead of multiplying it
Explanation:
The lock has a code that consists of 3 number
It is given that the number in the lock code can be used between
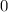 to
to
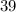
Thus, out of total
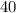 set of numbers (i.e
set of numbers (i.e
 ), the numbers can be repeated.
), the numbers can be repeated.
This means for all three code numbers the opportunity of choosing a number is same i.e. between

Now, the first digit of the code can be any number between

Like wise the second and third digit of the code can be any number between

Thus. the possible number of codes with repetition allowed are
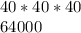
Hence, Jillian is not correct
Jillian has summed up the possible number of codes for each digit instead of multiplying it