Question

What is the area of the composite figure whose vertices have the following coordinates?

(−4, 3) , (2, 3) , (4, −1) , (0, −3) , (−2, −1)

Answer 1

30 square units

Explanation:

There are several ways to determine the area of the figure from its coordinates. A straightforward method is to plot the coordinates on a graph and decompose the resulting figure into simple shapes whose area formulas are known

Area from simpler shapes

A plot reveals the figure to be a parallelogram with a base length 6 and a height of 4, together with a triangle of base 6 and height 2.

The area of the parallelogram is given by the formula ...

A = bh

The area of the triangle is given by the formula ...

A = 1/2bh

In each case, 'b' represents the base of the figure, and 'h' represents its height.

Parallelogram area

A = bh = (6)(4) = 24

Triangle area

A = 1/2bh = 1/2(6)(2) = 6

Total area

The composite area will be the sum of the parallelogram and triangle areas:

A = 24 +6 = 30 . . . . square units

The area of the composite figure is 30 square units.

__

Area from coordinates

The area can also be figured directly from the coordinates. The formula for that can be written ...

`\displaystyle A=(1)/(2)\left|\sum_(k=1)^n (x_k(y_(k+1)-y_(k-1)))\right|\qquad\text{where $y_0=y_n$ and $y_(n+1)=y_1$}`

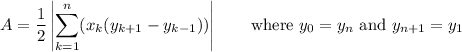
Using this formula, we find the area to be ...

A = 1/2|(-4(3-(-1)) +2(-1-3) +4(-3-3) +0(-1-(-1)) -2(3-(-3))|

= 1/2|-16 -8 -24 +0 -12| = 1/2|-60| = 30

The area of the figure is 30 square units.