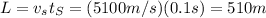Question

One end of a steel bridge is struck by a hammer. The sound produced is transmitted through the bridge and through the air to the other side of the bridge. There is a 1.4 s delay between the arrivals of the two sounds. What is the length of the bridge if the velocity of sound in air is 340 m/s and in steel is 5100 m/s. m

Answer 1

The sound in steel covers the distance L (length of the bridge) in a time
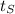
`t_S`, with a velocity
`v_S=5100 m/s`:

`v_S = (L)/(t_S)`
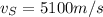
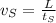
which we can rewrite as

`L=v_S t_S` (1)

Similarly, the sound in air covers the length of the bridge L in a time
`t_A`, with a velocity
`v_A=340 m/s`:

`v_A = (L)/(t_A)`
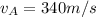
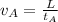
which we can rewrite as

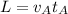
`L=v_A t_A` (2)
We also know that the sound in air arrives with a delay of 1.4 s. This means we can rewrite tA as

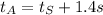
`t_A = t_S+1.4 s` (3)

The length of the bridge is always the same, so we can write (1)=(2) and using the information found in (3):

`v_A (t_S+1.4)=v_S t_S`
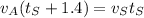
Re-arranging, we find

`t_S = (1.4 v_A )/(v_S -v_A)=0.1 s`

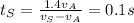
And at this point we can find the length of the bridge:

`L=v_s t_S = (5100 m/s)(0.1 s)=510 m`