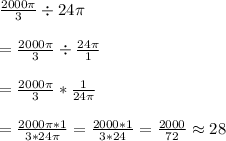Question

Please Help Me........

1. Ki’von has a sink that is shaped like a half-sphere. The sink has a diameter of 20 inches. One day, his sink clogged. He has to use one of two different cups to scoop the water out of the sink. The sink is completely full when Ki’von begins scooping.

(a) What is the exact volume of the sink? Show your work.

(b) One conical cup has a diameter of 8 in. and a height of 6 in. How many cups of water must Ki’von scoop out of the sink with this cup to empty it? Round the number of scoops to the nearest whole number. Show your work.

(c) One cylindrical cup has a diameter of 4 in. and a height of 6 in. How many cups of water must he scoop out of the sink with this cup to empty it? Round the number of scoops to the nearest whole number. Show your work.

Answer 1

The formula for the volume of a sphere is V=(4/3)πr³. We will only need half of this, so our formula is V=(1/2)(4/3)πr³=(4/6)πr³=(2/3)πr³. Since the diameter of the sink is 20 in, the radius is half of that or 10 in. Substituting that in, we have:
V=(2/3)π(10³)=(2/3)(1000)π=2000π/3 in³.

The formula for the volume of the conical cup is V=(1/3)πr²h. Our radius is 1/2 of the 8 in diameter, or 4 in. Using our information we have V=(1/3)π(4²)(6)=(1/3)π(96)=32π in³.

To find out how many cups it will take to empty the sink, we divide the volume of the sink by the volume of the cup:

`(2000\pi)/(3) / 32\pi \\ \\=(2000\pi)/(3) / (32\pi)/(1) \\ \\=(2000\pi)/(3) * (1)/(32\pi) \\ \\=(2000\pi *1)/(3*32\pi) \\ \\=(2000*1)/(3*32)=(2000)/(96) \approx 21`

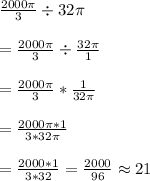
The volume of the cylindrical cup is given by the formula V=πr²h. Our radius is half of the diameter of 4, or 2 in. Using our information we have V=π(2²)(6)=24π in³. To determine how many cups it would take to empty the sink we divide the volume of the sink by the volume of the cup:

`(2000\pi)/(3) / 24\pi \\ \\=(2000\pi)/(3) / (24\pi)/(1) \\ \\=(2000\pi)/(3) * (1)/(24\pi) \\ \\=(2000\pi *1)/(3*24\pi)=(2000*1)/(3*24)=(2000)/(72) \approx 28`