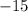Question

Find a1 for the arithmetic series with s20 = 80 And d = 2

Answer 1

To solve this, we are going to use the standard formula for arithmetic series
`S _(n) = (n)/(2) [2a_(1) +(n-1)d]`
where:

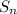
`S_(n)` is the sum of the arithmetic sequence

`n` is the number of terms

`d` is the difference

`a_(1)` is the first term
From our problem we know that
`S_(n) =80`,
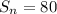
`n=20`, and
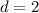
`d=2`. Lets replace those values in our formula to find
`a_(1)`:

`80= (20)/(2) [2a_(1) +(20-1)2]`

`80=10(2a_(1) +38)`

`80=20a_(1) +380`

`20a_(1) =-300`

`a_(1) = (-300)/(20)`

`a_(1) =-15`

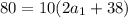
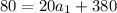
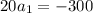
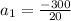
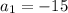
We can conclude that the first term
`a_(1)` of the arithmetic series is
`-15`

Answer 2

we know that
the formula of the arithmetic series is
Sn=n[2(a1) + (n - 1)d]/2
where
Sn=80
n=20
d=2
a1=?
then
80=20*[2*a1+19*2]/2----------------> 160=[40*a1+760]
160=[40*a1+760]----------> a1=(160-760)/40------------> a1=-15

the answer is
a1=-15