Question

If there is an 80% chance of rain and a 10% chance of wind and rain, what is the probability that it is windy, given that it is rainy? Round your answer to the nearest percent.

Answer 1

Required Probability = 0.125 or 12.5%

Explanation:

We are given that there is an 80% chance of rain and a 10% chance of wind and rain.

Let Probability of rain = P(R) = 0.80

and Probability of wind and rain =
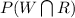`P(W \bigcap R)` = 0.10

We have to find the probability that it is windy, given that it is rainy i.e,; P(W/R)

Firstly, The conditional Probability P(A/B) is given by =
`(P(A \bigcap B))/(P(B))`

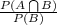
So, P(W/R) =
`(P(W \bigcap R))/(P(R))` =
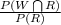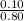`(0.10)/(0.80)` = 0.125 or 12.5%

Therefore, probability that it is windy, given that it is rainy is 12.5% .

Answer 2

The probability that it is windy, given that it is rainy is 0.13.

Explanation:

The conditional probability of an event B given that another event A has already occurred is,

`P(B|A)=(P(A\cap B))/(P(A))`

Denote the events as follows:

R = rainy weather

W = windy weather

Given:

P (R) = 0.80

P (W ∩ R) = 0.10

Compute the probability that it is windy, given that it is rainy as follows:

`P(W|R)=(P(W\cap R))/(P(R))=(0.10)/(0.80)=0.125\approx0.13`

Thus, the probability that it is windy, given that it is rainy is 0.13.