Question

Write the quadratic equation in factored form. Be sure to write the entire equation. x2 - 5x - 24 = 0

Answer 1

(x+3)(x-8)=0

Explanation:

Answer 2

​x² - 5x - 24 = 0

First, we have to solve the quadratic equation and find the two values of x that fit the equation.​

`x = \frac{5+- \sqrt{5^(2) + 4*1*24 } }{2*1} = (5+- √(25 + 96) )/(2) = (5+- √(121) )/(2) = (5+-11)/(2)`​

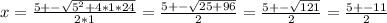
There are two values of x that fit:​

x₁ = (5+11)/2 = 16/2 = 8​

x₂ = (5-11)/2 = -6/2 = -3​

Now I can restate the original equation in terms of a product of factors, with this product being equal to zero:​

(x - x₁) * (x - x₂) = 0​

ANSWER ​(x-8) * (x+3) = 0

Now I can solve each factor by setting each one equal to zero and solving the resulting linear equations:​

x - 8 = 0 or x + 3 = 0​

x = 8 or x = -3​

We can check that these two values are the solution to the original quadratic equation.​

x² - 5x - 24 = 0​

​First value

​8² -5*8 -24 = 0

64 - 40 -24 = 0​

0 = 0 ¡Checked!​

Second value​

(-3)² -5(-3) -24 = 0​

9 + 15 -24 = 0​

0 = 0 ¡Checked!​

​Hope this helps!

​
`\textit{\textbf{Spymore}}`​​​