Question

A square has side lengths of 2x inches. An equilateral triangle has side lengths of (2x+1/3) inches. If the square and the triangle have the same perimeter, what is the value of x?

Answer 1

Size square × 4 = size triangle × 3
(2X × 4 ) = [(2X +1/3) × 3]

8X = [(6X+1)/3×3]
8X = 6X+1
8X -6X = 1
2X = 1
X= 1/2

Answer 2

Answer : The value of 'x' is
`(1)/(2)`

Step-by-step explanation :

As we know that,

The perimeter of square = 4a

The perimeter of equilateral triangle = 3s

('a' is the side square and 's' is the side of equilateral triangle)

Given:

Side of square = a = 2x

Side of equilateral triangle = s = (2x+1/3)

As per question, the square and the triangle have the same perimeter. That means,

Perimeter of square = Perimeter of equilateral triangle

4a = 3s

Now put the value of 'a' and 's', we get the value of 'x'.

`4* (2x)=3* (2x+(1)/(3))`

`8x=6x+1`

`8x-6x=1`

`2x=1`

`x=(1)/(2)`

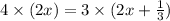
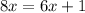
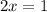
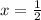
Therefore, the value of 'x' is
`(1)/(2)`