The probability that he got at least 2 questions correct is 0.756
Lets assume, the event of getting a question correct is P
As, each question has 4 answer choices and only one choice is correct,
So, P =

When
the probability of getting 1 success in 1 trial is p, then the probability of getting exactly x successes out of n trials is given by the
formula :
(ⁿCₓ )(P)ˣ (1-P)ⁿ⁻ˣ
Here the total number of questions is 10. So, n= 10
Stan needs to get at least 2 questions correct, that means he can get 2, 3, 4, 5, 6, 7, 8, 9 or 10 questions correct.
Now according to the formula,
P(x=2) = ¹⁰C₂ (
 )² (
)² (
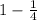 )¹⁰⁻²
)¹⁰⁻²
= ¹⁰C₂
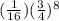
= 0.281567573
P(x=3) = ¹⁰C₃ (
 )³
)³
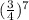
= (120) (
 )³
)³
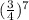
= 0.250282287
P(x=4) = ¹⁰C₄ (
 )⁴
)⁴
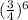
= (210)(
 )⁴
)⁴
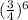
= 0.145998001
P(x=5) = ¹⁰C₅ (
 )⁵
)⁵
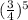
= (252) (
 )⁵
)⁵
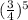
= 0.058399200
P(x=6) = ¹⁰C₆ (
 )⁶
)⁶
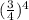
= (210) (
 )⁶
)⁶
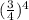
= 0.016222000
P(x=7) = ¹⁰C₇ (
 )⁷
)⁷

= (120) (
 )⁷
)⁷

= 0.003089904
P(x=8) = ¹⁰C₈ (
 )⁸
)⁸
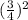
= (45) (
 )⁸
)⁸
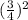
= 0.000386238
P(x=9) = ¹⁰C₉ (
 )⁹
)⁹
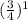
= (10) (
 )⁹
)⁹
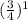
= 0.000028610
P(x=10) = ¹⁰C₁₀ (
 )¹⁰
)¹⁰
= 0.000000953
Now we will just add all the probabilities and get:
0.281567573 + 0.250282287+ 0.145998001+ 0.058399200+ 0.016222000+0.003089904+0.000386238+ 0.000028610 +0.000000953
= 0.755974766
= 0.756 (rounding to the nearest thousandth)
So, the probability that he got at least 2 questions correct is 0.756