Question

A merry-go-round is spinning at a rate of 4.0 revolutions per minute. cora is sitting 1.0 m from the center of the merry-go-round and cameron is sitting right on the edge, 2.0 m from the center. what is the relationship between the rotational speeds of the two children?

Answer 1

Same.

Step-by-step explanation:

The rotational speed of an object is given by :

`\omega=(\theta)/(t)`

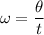
`\theta` is the angular displacement

t is the time taken

The angular speed of a merry- go- round is 4 revolutions per minute. There are two persons Cora and Cameron. Cora is sitting 1.0 m from the center of the merry-go-round and Cameron is sitting right on the edge, 2.0 m from the center.

The rotational speeds of both of the children remains the same because it is independent of the distance from the center.

Answer 2

The rotational speed of the two children is the same.
In fact, it is defined as

`\omega = (\Delta \theta)/(\Delta t)`
where
`\Delta \theta` is the angle covered in the time
`\Delta t`. As it can be seen, this quantity does not depend on the distance from the centre, so the rotational speed is 4.0 revolutions per minute for both children.