Answer: The required sum is 504.
Step-by-step explanation: We are given to find the sum of the following arithmetic series using the formula for the sum of an arithmetic series :
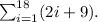
The given arithmetic series can be written, in expanded form, as follows :
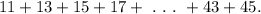
We know that
the sum of first n terms of an arithmetic series with first term a and common difference d is given by
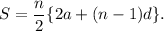
In the given series, a = 11 and d = 13 - 11 = 15 - 13 = . . . =2.
Therefore, the sum up to 18 terms will be
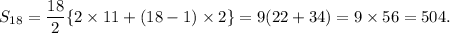
Thus, the required sum is 504.