Question

What is the sum of the arithmetic series below? Use the formula for the sum of an arithmetic series.

Answer 1

Answer: The required sum is 504.

Step-by-step explanation: We are given to find the sum of the following arithmetic series using the formula for the sum of an arithmetic series :

`\sum_(i=1)^(18)(2i+9).`

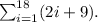
The given arithmetic series can be written, in expanded form, as follows :

`11+13+15+17+~.~.~.~+43+45.`

We know that

the sum of first n terms of an arithmetic series with first term a and common difference d is given by

`S=(n)/(2)\{2a+(n-1)d\}.`

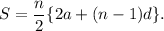
In the given series, a = 11 and d = 13 - 11 = 15 - 13 = . . . =2.

Therefore, the sum up to 18 terms will be

`S_(18)=(18)/(2)\{2* 11+(18-1)*2\}=9(22+34)=9*56=504.`

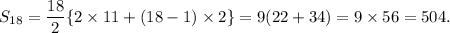
Thus, the required sum is 504.