Question

At the school carnival, the sixth graders are making directional arrows, as shown below.

Each arrow is to be painted red. How much area needs to be painted for 1 arrow?

26 square inches
29 square inches
32 square inches
44 square inches

Answer 1

We can separate this into a rectangle and a triangle and then find the areas of these shapes separately. The triangle has a height of 9 - 5 = 4 inches, and a base of 6 inches. The rectangle will have a width of 4 inches and a length of 5 inches. Use the formulas to find the areas of these shapes and then combine them to find the area of the entire arrow:

Triangle:


`\sf A=(1)/(2)bh`


`\sf A=(1)/(2)(6)(4)`


`\sf A=12~in^2`

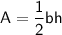
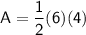
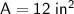
Rectangle:


`\sf A=lw`


`\sf A=(5)(4)`


`\sf A=20~in^2`

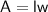
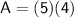
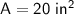
Now add the two areas together:


`\sf 20+12=\boxed{\sf 32~in^2}`

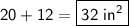
So your answer is C.