Question

The image on a movie poster was shrunk to make the DVD cover art for the movie, so that the cover art is a scale image of the poster. The poster is 36 inches wide, and the DVD cover art is 6 inches wide. If the diagonal of the poster is 4 feet, what is the diagonal of the DVD cover art?

Answer 1

Please see the attached image for a visual representation of our scale factor. We can set up this proportion by taking the DVD cover and poster values and placing them in fractions. Cross multiply and divide to solve for x. 

Answer 2

The first thing we need to do is find the proportionality constant
`k`. Since we now that the width of a movie poster was shrunk from 36 inches to 6 inches to make the DVD cover,
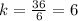
`k= (36)/(6) =6`; therefore, the width of poster was shrunk, in other words divided, by a factor of 6.
Now that we have our proportionality constant lest apply it to the diagonal of the poster to find the diagonal of the DVD cover. But notice that the diagonal of the poster is in feet not inches, so we need to convert 4 feet to inches first. Remember that 1 foot = 12 inches, so lets use that proportion to set up our conversion fraction:

`(4feet)( (12inches)/(1 foot) )= 48inches`
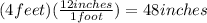
The only thing left now is shrunk, divide, the diagonal by our proportionality constant
`k`

`(48)/(k) = (48)/(6) =8`

We can conclude that If the diagonal of the poster is 4 feet, the diagonal of the DVD cover will be 8 inches.