Question

A small plane leaves an airport at a speed of 252 miles per hour. A jet leaves the airport 2 hours later traveling at 672 miles per hour. How long will the small plane be flying before the jet catches up to it? What unit will you use for your answer?

Answer 1

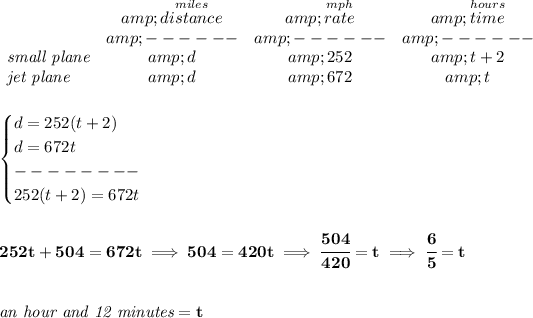
recall your d = rt, distance = rate * time.

the small plane runs at a rate of 252 mph, the jet runs at 672 mph, but the jet takes off 2 hours later.

if the jet plane say has been traveling for "t" hours by the time they meet, the small plane was already rolling before the jet, actually 2 hours earlier, so if the jet has gone for "t" hours, the small plane has been going for "t+2" hours.

now, by the time they both meet, the distance covered by say the small plane is "d" miles, but the distance covered by the jet is also the same "d" miles, since they're meeting.


`\bf \begin{array}{lccclll} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ &------&------&------\\ \textit{small plane}&d&252&t+2\\ \textit{jet plane}&d&672&t \end{array} \\\\\\ \begin{cases} d=252(t+2)\\ d=672t\\ --------\\ 252(t+2)=672t \end{cases} \\\\\\ 252t+504=672t\implies 504=420t\implies \cfrac{504}{420}=t\implies \cfrac{6}{5}=t \\\\\\ \textit{an hour and 12 minutes}=t`

Answer 2

No, thanks to you, I got the question wrong it was hours.