Question

A spring is compressed to a displacement of -3.9 m from equilibrium. Then the spring is released and allowed to stretch to a displacement of -1.5 m from equilibrium. The spring constant is 11 N/m. What best describes the work involved as the spring stretches? 71 J of work is performed on the spring. The spring performs 140 J of work The spring performs 71 J of work. 140 J of work is performed on the spring.

Answer 1

The elastic potential energy stored by a spring is

`U= (1)/(2) k x^2`
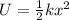
where
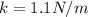
`k=1.1 N/m` is the spring's constant and x is the displacement of the spring with respect its rest position.

In the problem we have two situations: situation 1 (initial condition), where the spring has a displacement of
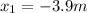
`x_1 = -3.9 m`, and situation 2 (final condition), where the spring has a displacement of
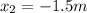
`x_2 = -1.5 m`. The work performed by the spring corresponds to its loss in elastic potential energy:

`W=U_1- U_2 = (1)/(2)kx_1^2- (1)/(2)kx_2^2 = (1)/(2)k[x_1^2-x_2^2]=`

`= (1)/(2)(1.1 N/m)[(-3.9m)^2-(-1.5m)^2]=71 J`
this work has positive sign, because it is performed by the spring (in factm the spring is releasing from a position of higher potential energy to a position with less potential energy).

Therefore, the correct answer is The spring performs 71 J of work.