Answer with explanation:
1.⇒ The given equation is
5x-2y=3
For one solution ,you should write linear equation in such a way
ax+by=c, such that
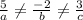
So, the linear equation will be
→3x+4y=8
You can write many more by yourself.
2.⇒Exactly two solutions
The two lines intersect at only one point.So,there are no such lines which has two point of Intersection.
3.⇒No solutions
It means the two lines will never intersect.
For no solution ,you should write equation of line in such a way
ax+by=c, such that
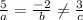
So, the linear equation will be
→10x -4y=15
You can write many more by yourself.
4.⇒Infinitely many solutions
For Infinite number of solution ,you should write linear equation in such a way
ax+by=c, such that
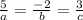
→10x-4y=6