Question

What is the area of this figure?

Select from the drop-down menu to correctly complete the statement.

The area of the figure is ? cm2.

A. 102
B. 132
C. 168
D. 340

SOMEONE PLEASE HELP ASAP!!

Answer 1

First of all we can draw a parallel line to divide the figure into a triangle and a rectangle as shown in the figure. To find the area of our rectangle, remember that the area of a rectangle is length times width, so
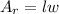
`A_(r) =lw`. Since we know for our figure that the length and width of our rectangle are 13cm and 6cm respectively, lets replace those values in our formula to get its area:

`A _(r) =(13cm)(6cm)`

`A=78cm^(2)`
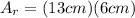
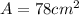
Similarly, the area of a triangle is one half times base times height, so
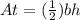
`At=( (1)/(2))bh`. Since we know that our base is 8cm and our height 6cm, lets replace those values in our equation to find the area of our triangle:

`A_(t) =( (1)/(2))(8cm)(6cm)`

`A_(t) =24cm^(2)`

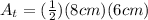
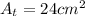
Now the only thing left is add our areas:

`A_(total) =78cm^(2)+24cm^(2) =102cm^(2)`

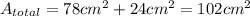
We can conclude that the correct answer is A. 102