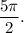Answer: The required measures of two angles one positive and negative that are co-terminal with
 are
are
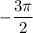 and
and
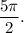
Step-by-step explanation: We are given to find measures of two angles one positive and negative that are co-terminal with

Let x and y represents the positive and negative co-terminal angles respectively.
We know that
the measures of any two co-terminal angles differ from each other by a multiple of
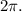
So, the values of x and y can be found as follows :
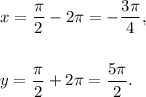
Thus, the required measures of two angles one positive and negative that are co-terminal with
 are
are
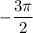 and
and