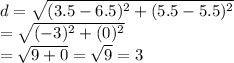Since RS is a midsegment parallel to AC, that means R is the midpoint of AB and S is the midpoint of BC. The midpoint formula is:
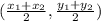
. Using the coordinates of A and B, we have:

. Similarly, S is the midpoint of BC:

.
Since ST is a midsegment parallel to AB, then T must be a midpoint of AC:

.
Now that we have the coordinates of each point we can find the length of each segment using the distance formula:

For ST:
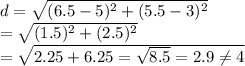
For RT:
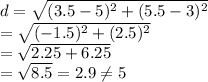
For RS: