Part A: We know that the equation for finding the area of a triangle is
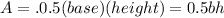
; we also know that
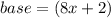
and
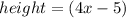
, so the only thing we need to do is replacing those values into our Area equation and solve for x:
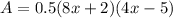
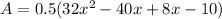
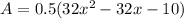
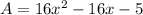
Now the only thing left is factor the quadratic polynomial:
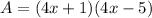
W can conclude that the area of our triangle is
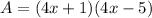 Part B:
Part B: Our polynomial has three terms, so is a trinomial; also, our polynoal only has one variable,

, and the largest exponent of that variable is 2; therefore is a degree 2 polynomial. In summary, we have a
trinomial of degree 2. Part C: Part A demonstrate the closure property of polynomials because after multiplying tow polynomials we obtained another polynomial.