Question

a person walking along a straight road observes that at two consecutive kilometer stones, the angles of elevation of a hill in front of him are 30degree and 45 degree find the height of the hill

Answer 1

First, you need to draw the situation: you have three points on a straight line, A is the first kilometer stone, B is the second one and C is the foot of the hill. Let's call H the top of the hill. Connecting H with both A and B you get two triangles rectangle (BCH and ACH).

The triangle rectangle BCH has one other angle that is 45°, which means that it is an isosceles triangle, therefore BC = HC = height of the hill (h).

Now, consider the triangle ACH: it has an angle of 30° (which means that the other angle is 60°) and AC = BC + AB = h + 1 (where we considered h measured in km).
In such a particular triangle (30°- 60°- 90°), the ratio between the long and the short leg is √3, which means that:
√3·HC = AC

We can then write:
√3·h = (h + 1)

which can be solve for h:
√3·h - h = 1
h(√3 - 1) = 1
h =1/ (√3 - 1)

We can rationalize:
h =
`(1)/( √(3) - 1) ( √(3) + 1)/( √(3) + 1 )`
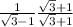
= (√3 + 1) / 2
= 1.366 km

Therefore the correct answer is: the hill is 1.366km high