Answer: Our factorized term will be
2xy(2x+5)(2x-3)
Step-by-step explanation:
Since we have given that
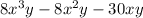
All we need to do is to factorise this expression.
Here are the steps given below:

By manipulating the terms, we get:
![2xy[(2x)^2-4x+1-16]\\\\2xy[(2x-1)^2-16]\\\\2xy[(2x-1)^2-(4)^2]\\\\2xy[(2x-1-4)(2x-1+4)]\\\\2xy[(2x-5)(2x+3)]](https://img.qammunity.org/2019/formulas/mathematics/college/mg8dzmi5w98uofsycskt53gnhtg0tfkrbh.png)
Alternatively,
By using splitting the middle terms,
![2xy(4x^2-4x-15)\\\\2xy(4x^2-10x+6x-15)\\\\2xy[2x(2x-5)+3(2x-5)]\\\\2xy(2x-3)(2x+5)](https://img.qammunity.org/2019/formulas/mathematics/college/mwx646h2tw16ej52qs52l6p3b54vl0b08n.png)
Hence, our factorized term will be
2xy(2x+5)(2x-3)