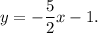Question

What is the equation of the line that is parallel to the line 5x + 2y = 12 and passes through the point (−2, 4)? y = – x – 1y = – x + 5y = x – 1y = x + 5

Answer 1

the equation of the line parallel to 5x+2y=12 and passes through the point (-2, 4) is equal to y= -5/2x - 1

Answer 2

Answer: The required equation of the line is
`y=-(5)/(2)x-1.`

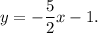
Step-by-step explanation: We are given to find the equation of the line that is parallel to the following line and passes through the point (-2, 4) :

`5x+2y=12~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We know that

the slope-intercept form of the equation of a straight line is given by

`y=mx+c,`

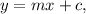
where m is the slope of the line.

From equation (i), we have

`5x+2y=12\\\\\Rightarrow 2y=-5x+12\\\\\Rightarrow y=-(5)/(2)x+6.`

So, the slope of line (i) is given by

`m=-(5)/(2).`

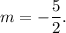
We know that the slopes of two parallel lines are equal. So, the slope of the new line will be

`m=-(5)/(2).`

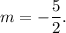
Since the line passes through the point (-2, 4), so its equation will be

`y-4=m(x-(-2))\\\\\\\Rightarrow  y-4=-(5)/(2)(x+2)\\\\\\\Rightarrow y-4=-(5)/(2)x-5+4\\\\\\\Rightarrow y=-(5)/(2)x-1.`

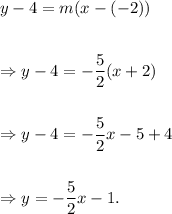
Thus, the required equation of the line is
`y=-(5)/(2)x-1.`