Question

Helpppppppppppppppppppppppppppppppppppp

Answer 1

First we rewrite the expression:
root (8x ^ 7y ^ 8)
(8x ^ 7y ^ 8) ^ (1/2)
Properties of exponents:
(8 ^ (1/2) x ^ (7/2) y ^ (8/2)
We rewrite:
(8 ^ (1/2) x ^ (7/2) y ^ 4
(2 * 2 ^ (1/2) x ^ 3y ^ 4x ^ (1/2)
(2 * x ^ 3 * y ^ 4 * (2x) ^ (1/2)
Answer:
(2*x^3*y^4*(2x)^(1/2)
option 3

Answer 2

To take out terms outside the radical we need to divide the power of the term by the index of the radical; the quotient will be the power of the term outside the radical, and the remainder will be the power of the term inside the radical.
First, lets factor 8:

`8=2 ^(3)`
Now we can divide the power of the term, 3, by the index of the radical 2:

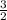
`(3)/(2)` = 1 with a remainder of 1
Next, lets do the same for our second term
`x^(7)`:

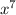
`(7)/(2)` = 3 with a remainder of 1
Again, lets do the same for our third term
`y^(8)`:

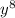
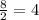
`(8)/(2) =4` with no remainder, so this term will come out completely.

Finally, lets take our terms out of the radical:

`\sqrt{8x^(7) y^(8) }= \sqrt{ 2^(3) x^(7) y^(8) } =2 x^(3) y^(4) √(2x)`

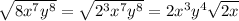
We can conclude that the correct answer is the third one.