Answer:
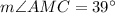 and
and
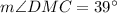 .
.
Explanation:
As you can observe in the image attached, angles AMC and DMC are congruent, because if point C is the incenter of AMD, that means each line the forms such point is a bisector.
Remember that a bisector is a line that equally divides an angle.
So,
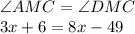
Solving for
 , we have
, we have

Then, we substitute this value in each expression to find the angles.
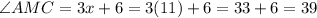
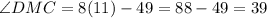
Therefore, the measures of those angles are
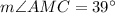 and
and
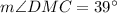 .
.