Question

`(2)/(10) = (4)/(a-3)`

Solve the proportion, then leave the fraction in a fraction as simplest form. Thanks! :)

Answer 1

Step-1: Use cross multiplication

• 
  `(2)/(10) = (4)/(a - 3)`
• 
  `2(a - 3) = 4(10)`

Step-2: Simplify both sides

• 
  `2(a - 3) = 4(10)`
• 
  `2a - 6 = 40`

Step-3: Add 6 both sides

• 
  `2a - 6 + 6 = 40 + 6`
• 
  `2a = 46`

Step-4: Divide 2 both sides

• 
  `2a = 46`
• =>
  `(2a)/(2) = (46)/(2)`
• =>
  `a = 23`

Double-check:

Step-1: Substitute the value of a into the proportion

• 
  `(2)/(10) = (4)/(a - 3)`
• =>
  `(2)/(10) = (4)/(23 - 3)`
• =>
  `(2)/(10) = (4)/(20)`

Step-2: Simplify both sides.

• 
  `(2)/(10) = (4)/(20)`
• =>
  `(1)/(5) = (1)/(5) (Correct)`

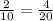
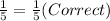
The value of a must be 23 to make the proportion true.

Answer 2

`\displaystyle a = 23`

General Formulas and Concepts:

Math

• Simplifying

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Explanation:

Step 1: Define

`\displaystyle (2)/(10) = (4)/(a - 3)`

Step 2: Solve for a

1. [Proportion] Simplify fraction:
   `\displaystyle (1)/(5) = (4)/(a - 3)`
2. [Multiplication Property of Equality] Cross-multiply:
   `\displaystyle a - 3 = 20`
3. [Addition Property of Equality] Add 3 on both sides:
   `\displaystyle a = 23`

Here we see that in order for the proportion to be equal, a must equal 23. Plugging in a back into the proportion should yield us a fraction equivalent to the original fraction.