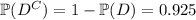Question

Hdc produces microcomputer hard drives at four different production facilities (f1, f2, f3, and f4) hard drive production at f1, f2, f3, and f4 is 20%, 25%, 15%, and 40%, respectively. quality control records indicate that 1.5%, 2%, 1%, and 3% of the hard drives are defective at f1, f2, f3, and f4, respectively.

a. if a defective hdc hard drive is picked at random, what is the probability that it was produced at f2?
b. if a defective hdc hard drive is picked at random, what is the probability that it was produced at f4?
c. if an hdc hard drive is picked at random, what is the probability that it is non-defective? g

Answer 1

Let
`D` denote the event that an HD is defective, and
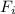
`F_i` the event that a particular HD was produced at facility
`i`.

You are asked to compute


`\mathbb P(F_2\mid D)`

`\mathbb P(F_4\mid D)`

`\mathbb P(D^C)`

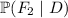
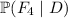
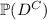
From the definition of conditional probabilities, the first two will require that you first find
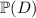
`\mathbb P(D)`. Once you have this, part (c) is trivial.

I'll demonstrate the computation for part (a). Part (b) is nearly identical.

(a)

`\mathbb P(F_2\mid D)=(\mathbb P(F_2\cap D))/(\mathbb P(D))`

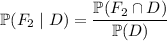
Presumably, the facility responsible for producing a given HD is independent of whether the HD is defective or not, so
`\mathbb P(F_2\cap D)=\mathbb P(F_2)\mathbb P(D)=0.20*0.015`.

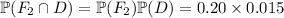
Use the law of total probability to determine the value of the denominator:


`\mathbb P(D)=\mathbb P(D\mid F_1)+\mathbb P(D\mid F_2)+\mathbb P(D\mid F_3)+\mathbb P(D\mid F_4)`

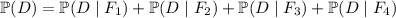
We know each of the component probabilities because they are given explicitly: 0.015, 0.02, 0.01, and 0.03, respectively. So


`\mathbb P(D)=0.015+0.02+0.01+0.03=0.075`

and thus


`\mathbb P(F_2\mid D)=(0.2*0.015)/(0.075)=0.04`

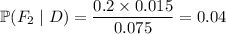
(b) Similarly,

`\mathbb P(F_4\mid D)=(0.4*0.03)/(0.075)=0.16`

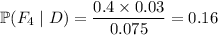
(c)

`\mathbb P(D^C)=1-\mathbb P(D)=0.925`