Looks like the PMF is supposed to be
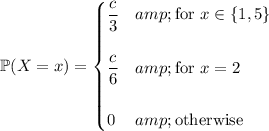
which is kinda weird, but it's not entirely clear what you meant...
Anyway, assuming the PMF above, for this to be a valid PMF, we need the probabilities of all events to sum to 1:
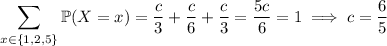
Next,
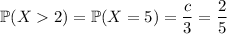
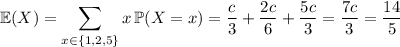
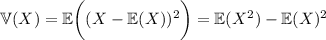

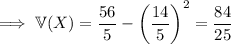
If
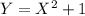
, then
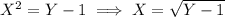
, where we take the positive root because we know
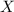
can only take on positive values, namely 1, 2, and 5. Correspondingly, we know that
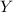
can take on the values
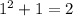
,
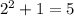
, and
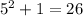
. At these values of
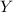
, we would have the same probability as we did for the respective value of
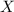
. That is,
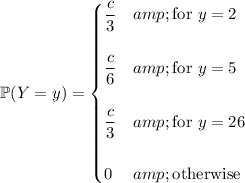
Part (5) is incomplete, so I'll stop here.