The question is incomplete, here is the complete question:
A solution is made by mixing 45.0 mL of ethanol,
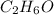 , and 55.0 mL of water. Assuming ideal behavior, what is the vapor pressure of the solution at 20 °C?
, and 55.0 mL of water. Assuming ideal behavior, what is the vapor pressure of the solution at 20 °C?
Constants @ 20°C:
ethanol = 0.789 g/mL (Density) & 43.9 Torr (Vapor Pressure)
water = 0.998 g/mL (Density) & 17.5 Torr (Vapor Pressure)
Answer: The vapor pressure of the solution at 20°C is 23.4 Torr
Step-by-step explanation:
To calculate the mass of substance, we use the equation:
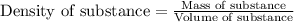 ......(1)
......(1)
To calculate the number of moles, we use the equation:
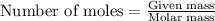 .....(2)
.....(2)
Mole fraction of a substance is given by:
 ......(3)
......(3)
Density of ethanol = 0.789 g/mL
Volume of ethanol = 48.0 mL
Putting values in equation 1, we get:
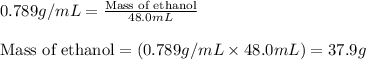
Given mass of ethanol = 37.9 g
Molar mass of ethanol = 46 g/mol
Putting values in equation 2, we get:
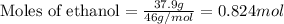
Density of water = 0.998 g/mL
Volume of water = 52.0 mL
Putting values in equation 1, we get:
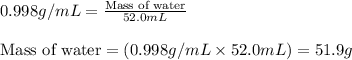
Given mass of water = 51.9 g
Molar mass of water = 18 g/mol
Putting values in equation 2, we get:
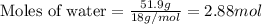
Calculating the mole fractions by using equation 3:
Mole fraction of ethanol,
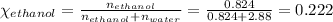
Mole fraction of water,
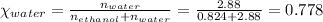
To calculate the total pressure of the mixture of the gases, we use the equation given by Raoult's law, which is:
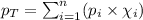

Putting values in above equation, we get:
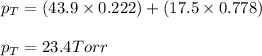
Hence, the vapor pressure of the solution at 20°C is 23.4 Torr