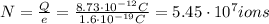Question

Suppose that the resistance between the walls of a biological cell is 6.8 × 109 ω. (a) what is the current when the potential difference between the walls is 69 mv? (b) if the current is composed of na+ ions (q = +e), how many such ions flow in 0.86 s?

Answer 1

(a) We can find the current flowing between the walls by using Ohm's law:

`I= (\Delta V)/(R)`
where
`\Delta V=69 mV=0.069 V` is the potential difference and
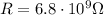
`R=6.8\cdot 10^9 \Omega` is the resistance. Substituting these values, we get

`I=1.01 \cdot 10^(-11) A`

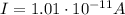
(b) The total charge flowing between the walls is the product between the current and the time interval:

`Q=I \Delta t`
The problem says
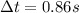
`\Delta t=0.86 s`, so the total charge is

`Q=(1.01\cdot 10^(-11) A)(0.86 s)=8.73 \cdot 10^(-12) C`

The current consists of Na+ ions, each of them having a charge of
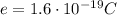
`e=1.6 \cdot 10^(-19) C`. To find the number of ions flowing, we can simply divide the total charge by the charge of a single ion:

`N= (Q)/(e) = (8.73 \cdot 10^(-12)C)/(1.6 \cdot 10^(-19)C) = 5.45 \cdot 10^7 ions`