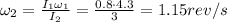Question

Suppose that the moment of inertia of a skater with arms out and one leg extended is 3.0 kg⋅m2 and for arms and legs in is 0.80 kg⋅m2 . if she starts out spinning at 4.3 rev/s , what is her angular speed (in rev/s) when her arms and one leg open outward?

Answer 1

Since no external torques are acting on the skater, his angular momentum must be conserved in the two different situations (arms and legs in - arms out and one leg out). The angular momentum is given by

`L=I \omega`
where I is the moment of inertia and
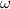
`\omega` the angular speed.

Labeling with "1" the situation where the skater has arms and legs in, and with "2" the situation where the skater has arms out and one leg out, the conservation of the angular momentum becomes

`L_1 = L_2`
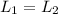
or

`I_1 \omega_1 = I_2 \omega _2`
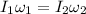
We know the moment of inertia and the angular speed of the skater when he has arms and legs in:

`I_1 = 0.80 kg m^2`

`\omega _1=4.3 rev/s`
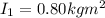
and also the moment of inertia of the skater when he has arms and one leg out:

`I_2 = 3 kg m^2`
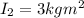
so we can find his angular speed when he opens the arms and one leg:

`\omega _2 = (I_1 \omega _1)/(I_2)= (0.8 \cdot 4.3)/(3) =1.15 rev/s`