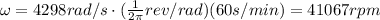The acceleration experienced by the particle is given by

This corresponds to the centripetal acceleration of the motion, which is related to the angular speed
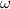
of the particle and its distance r from the axis by the relationship
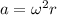
In our problem,
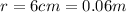
, so we can solve for
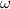
:

However, we must convert it into rpm (revolution per minute).
We know that 1 rad corresponds to
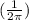
revolutions, while
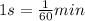
. So we the conversion is