Question

Which of the six trigonometric functions do not depend on the value of r?

Answer 1

If we construct a triangle in a circle of radius
`r`, the radius of the circle will be the hypotenuse of our triangle, and the legs will be
`x` and
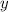
`y` as you can see in the picture.
Now we can construct our trigonometric ratios for our triangle as usual:

`sin \alpha = (y)/(r)`

`cos \beta = (x)/(r)`

`tan \beta = (y)/(x)`

`csc \beta = (r)/(y)`

`sec \beta = (r)/(x)`

`cot \beta = (x)/(y)`

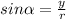
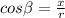
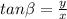
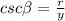
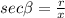
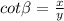
As you can see the only two trigonometric functions that don't depend on the value of
`r` are tangent and cotangent.