Question

Assume the second cart moves in the negative direction. two carts with masses of 4.6 kg and 3.3 kg move toward each other on a frictionless track with speeds of 5.1 m/s and 4.9 m/s, respectively. the carts stick together after colliding head-on. find their final speed. answer in units of m/s.

Answer 1

The total momentum of the system (cart 1+ cart 2) is conserved after the collision.
The initial momentum is

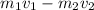
`m_1 v_1 - m_2 v_2` (1)
where the negative sign in front of cart 2 momentum is due to the fact it goes in the opposite direction of cart 1.
The final momentum is

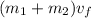
`(m_1 + m_2) v_f` (2)
because the two carts stick together, therefore their total mass is (m1+m2) moving at the new speed vf.

By requiring that (1) is equal to (2), we can solve to find the final speed vf:

`m_1 v_1 - m_2 v_2 = (m_1 + m_2) v_f`

`v_f = (m_1 v_1 - m_2 v_2)/(m_1+m_2)= ((4.6 kg)(5.1 m/s)-(3.3 kg)(4.9 m/s))/(4.6 kg+3.3 kg) =0.9 m/s`
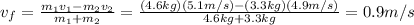
where the positive sign means the two carts are now going in the positive direction (i.e. the initial direction of cart 1)