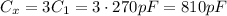Question

A circuit contains a single 270-pf capacitor hooked across a battery. it is desired to store four times as much energy in a combination of two capacitors by adding a single capacitor to this one. what would this value be

Answer 1

The energy stored by a system of capacitors is given by

`U= (1)/(2)C_(eq) V^2`
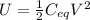
where Ceq is the equivalent capacitance of the system, and V is the voltage applied.

In the formula, we can see there is a direct proportionality between U and C. This means that if we want to increase the energy stored by 4 times, we have to increase C by 4 times, if we keep the same voltage.

Calling
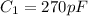
`C_1 = 270 pF` the capacitance of the original capacitor, we can solve the problem by asking that, adding a new capacitor with
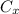
`C_x`, the new equivalent capacitance of the system
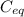
`C_(eq)` must be equal to
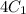
`4C_1`. If we add the new capacitance X in parallel, the equivalent capacitance of the new system is the sum of the two capacitance

`C_(eq) = C_1 + C_x`
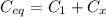
and since Ceq must be equal to 4 C1, we can write

`C_1+C_x = 4C_1`
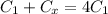
from which we find

`C_x=3C_1=3 \cdot 270 pF=810 pF`