Question

A school typically sells 500 yearbooks in a year for $50 each. The economics class does a project and discovers that they can sell150 more yearbooks for every $5 decrease in price. The revenue for yearbook sales is R(x) = (500 + 125x)(50 -5x).

1.) To maximize profit, what price should the school charge for the yearbooks? (Choose one of the multiple choice)
a) 35
b) 40
c) 45
d) 50
2.) What is the possible maximum revenue? (Choose one of the multiple choice)
a) 25,000
b) 30,625
c) 43,750
3.) And if the school attains the maximum revenue, how many yearbooks will they sell? (Choose one of the multiple choice)
a) 500
b) 625
c) 750
d) 875

Answer 1

Multiplying the two pieces of the function together:

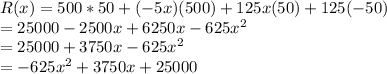
`R(x)=500*50 + (-5x)(500) + 125x(50) + 125(-50) \\=25000 -2500x+6250x-625x^2 \\=25000+3750x-625x^2 \\=-625x^2+3750x+25000`. This is a quadratic function, and since the coefficient of x² is negative we know it is opening downward and thus has a maximum. We can find the maximum by finding the vertex. First we find the axis of symmetry:

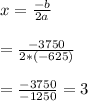
`x=(-b)/(2a) \\ \\=(-3750)/(2*(-625)) \\ \\=(-3750)/(-1250)=3`. This tell us there will need to be 3 $5 decreases in price, or a $15 decrease, to maximize the function. $50-$15=$35.
We now plug our 3 in for x in our function:

`R(x)=-625-(3^2)+3750(3)+25000 \\=-625(9)+11250+25000 \\=-5625+36250 \\=30,625`
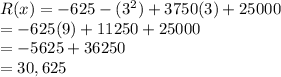
If they decrease the price their total revenue will be $30,625.
Looking at the function we know that they sell an extra 125 yearbooks for every $5 decrease in price. There were 3 $5 decreases, so 3(125) = 375 extra yearbooks. Add this to the original 500 and we have 375+500=875 yearbooks.