Question

A guy-wire is attached from the ground to the top of a pole for support. If the angle of elevation to the pole is 67° and the wire is attached to the ground at a point 137 feet from the base of the pole, what is the height of the pole (round to 2 decimal places)?

Answer 1

Answer:60.1

Explanation:

cos

Answer 2

The height of the pole is 322.75 feet.

Explanation:

Let the triangle Δ ABC with AC be the length of wire and AB be the Height of the pole

Length between the point of attachment of wire from base of the pole = BC = 137 feet

Angle of elevation to the pole = θ = 67°

We have to find the length of the pole that is AB Let the height of pole be h feet.

According to trigonometry :

`\tan C=\frac{\text{perpendicular}}{\text{base}}`

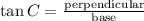
Here, C = 67° , perpendicular = AB = h , base = BC = 137

Substitute the values,

`\tan 67^(\circ)=(AB)/(BC)`

`\tan 67^(\circ)=(h)/(137)`

`h=\tan 67^(\circ) * 137`

`h=322.75`

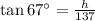
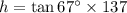
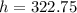
Thus, the height of the pole is 322.75 feet.